Zadanie nr 4794664
W trójkącie równoramiennym 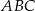 o podstawie
o podstawie 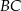 dane są:
dane są: 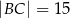 oraz
oraz 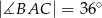 . Odcinek
. Odcinek 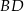 jest odcinkiem dwusiecznej kąta
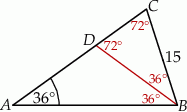
jest odcinkiem dwusiecznej kąta 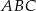 (zobacz rysunek).
(zobacz rysunek).
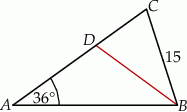
Wówczas długość odcinka 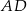 jest równa
jest równa
A) 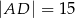 B)
B) 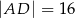 C)
C) 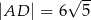 D)
D) 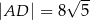
Rozwiązanie
Trójkąt 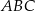 jest równoramienny, więc
jest równoramienny, więc
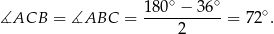
Odcinek 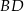 jest zawarty w dwusiecznej kąta
jest zawarty w dwusiecznej kąta 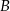 , więc
, więc
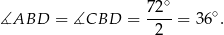
Stąd
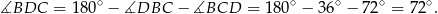
W szczególności trójkąty 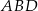 i
i 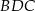 są równoramienne i
są równoramienne i 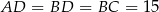 .
.
Odpowiedź: A

