Zadanie nr 5006206
Na bokach 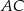 i
i 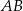 trójkąta
trójkąta 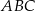 o wierzchołkach
o wierzchołkach 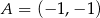 ,
, 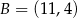 i
i 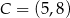 , wybrano punkty
, wybrano punkty 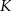 i
i 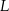 odpowiednio, w ten sposób, że
odpowiednio, w ten sposób, że 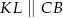 . Pole trapezu
. Pole trapezu 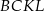 stanowi
stanowi 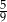 pola trójkąta
pola trójkąta 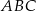 . Zatem
. Zatem
A) 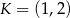 B)
B) 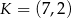 C)
C) 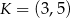 D)
D) 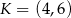
Rozwiązanie
Szkicujemy opisaną sytuację.
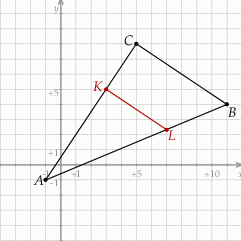
Wiemy, że pole trójkąta 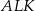 stanowi
stanowi
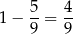
pola trójkąta 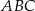 , więc
, więc 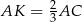 . Jeżeli oznaczymy
. Jeżeli oznaczymy 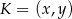 , to mamy
, to mamy
![−→ −→ AK = 2AC 3 2- [x + 1 ,y+ 1] = 3[5 + 1,8 + 1] = [4,6].](https://img.zadania.info/zad/5006206/HzadR6x.gif)
Stąd 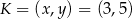 .
.
Odpowiedź: C

