Zadanie nr 5162557
Wysokość w trójkącie prostokątnym dzieli podstawę na odcinki o długościach 3 i 5. Pole tego trójkąta jest równe:
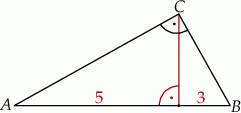
A) 15 B) 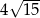 C) 16 D) za mało danych
C) 16 D) za mało danych
Rozwiązanie
Sposób I
Jak wiadomo, wysokość w trójkącie prostokątnym jest średnią geometryczną długości odcinków, na które wysokość ta dzieli przeciwprostokątną.
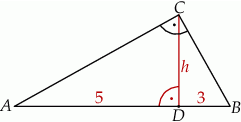
Mamy zatem 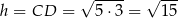 . Pole trójkąta jest więc równe
. Pole trójkąta jest więc równe
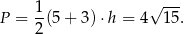
Sposób II
Zauważmy, że trójkąty 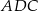 i
i 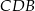 są podobne, więc
są podobne, więc
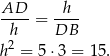
Pole trójkąta jest więc równe
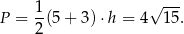
Odpowiedź: B

