Zadanie nr 5190589
W trójkącie prostokątnym o przyprostokątnych długości 6 i 8 połączono wierzchołek 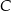 kąta prostego ze środkiem
kąta prostego ze środkiem 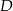 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 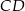 jest równa
jest równa
A) 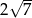 B) 10 C) 7 D) 5
B) 10 C) 7 D) 5
Rozwiązanie
Ponieważ trójkąt jest prostokątny, punkt 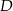 jest środkiem okręgu opisanego.
jest środkiem okręgu opisanego.
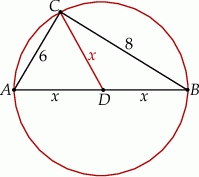
Zatem 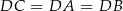 i jest to po prostu połowa długości przeciwprostokątnej. Długość przeciwprostokątnej wyliczamy z twierdzenia Pitagorasa
i jest to po prostu połowa długości przeciwprostokątnej. Długość przeciwprostokątnej wyliczamy z twierdzenia Pitagorasa
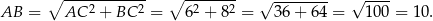
Szukana długość odcinka 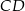 to połowa tej długości.
to połowa tej długości.
Odpowiedź: D

