Zadanie nr 5586016
Dany jest kąt 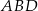 o mierze
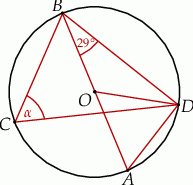
o mierze 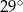 (rys.). Kąt
(rys.). Kąt 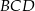 ma miarę:
ma miarę:
A) 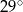 B)
B) 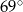 C)
C) 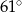 D)
D) 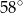
Rozwiązanie
Sposób I
Odcinek 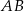 jest średnicą okręgu, więc trójkąt
jest średnicą okręgu, więc trójkąt 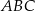 jest prostokątny. Stąd
jest prostokątny. Stąd
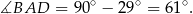
Kąty 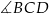 i
i 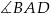 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
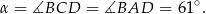
Sposób II
Trójkąt 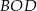 jest równoramienny, więc
jest równoramienny, więc
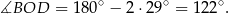
Korzystamy teraz z tego, że kąt wpisany jest dwa razy mniejszy od kąta środkowego opartego na tym samym łuku.
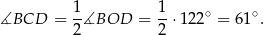
Odpowiedź: C

