Zadanie nr 5740786
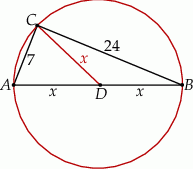
W trójkącie prostokątnym o przyprostokątnych długości 7 i 24 połączono wierzchołek 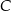 kąta prostego ze środkiem
kąta prostego ze środkiem 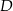 przeciwprostokątnej. Długość odcinka
przeciwprostokątnej. Długość odcinka 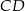 jest równa
jest równa
A) 25 B) 12 C) 15 D) 12,5
Rozwiązanie
Ponieważ trójkąt jest prostokątny, punkt 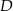 jest środkiem okręgu opisanego.
jest środkiem okręgu opisanego.
Zatem 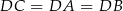 i jest to po prostu połowa długości przeciwprostokątnej. Długość przeciwprostokątnej obliczamy z twierdzenia Pitagorasa
i jest to po prostu połowa długości przeciwprostokątnej. Długość przeciwprostokątnej obliczamy z twierdzenia Pitagorasa
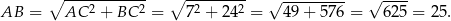
Szukana długość odcinka 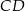 to połowa tej długości.
to połowa tej długości.
Odpowiedź: D

