Zadanie nr 5743384
Dany jest trójkąt prostokątny o kącie prostym przy wierzchołku 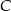 . Środkowa
. Środkowa 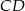 tworzy z przyprostokątną
tworzy z przyprostokątną 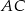 kąt
kąt 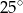 . Wynika stąd, że kąt między tą środkową a wysokością
. Wynika stąd, że kąt między tą środkową a wysokością 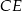 trójkąta ma miarę
trójkąta ma miarę
A) 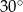 B)
B) 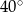 C)
C) 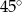 D)
D) 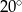
Rozwiązanie
Zaczynamy od rysunku
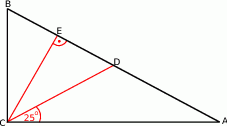
Sposób I
Ponieważ punkt 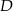 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 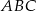 , więc
, więc 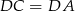 , czyli trójkąt
, czyli trójkąt 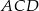 jest równoramienny. Mamy zatem
jest równoramienny. Mamy zatem
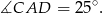
Patrzymy teraz na trójkąt prostokątny 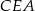
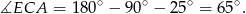
Zatem
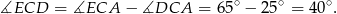
Sposób II
Jak zauważyliśmy w poprzednim sposobie, punkt  jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie  , skąd
, skąd 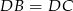 . Ponadto
. Ponadto
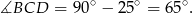
Trójkąt 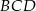 jest więc równoramienny i jeden z jego kątów ma miarę
jest więc równoramienny i jeden z jego kątów ma miarę 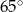 , więc
, więc
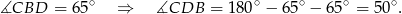
Zatem z trójkąta 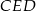 mamy
mamy
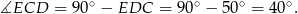
Odpowiedź: B

