Zadanie nr 6438788
Przekątna sześcianu jest o 5 większa od przekątnej ściany sześcianu. Wówczas krawędź sześcianu jest równa
A) 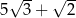 B)
B) 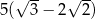 C)
C) 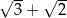 D)
D) 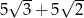
Rozwiązanie
Zaczynamy od rysunku
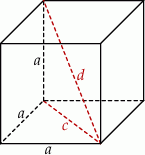
Z twierdzenia Pitagorasa wyznaczamy długość przekątnej ściany
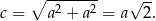
Podobnie wyznaczamy długość przekątnej sześcianu
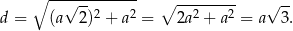
Korzystamy z założenia i otrzymujemy równanie
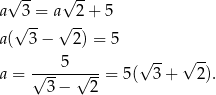
Odpowiedź: D

