Zadanie nr 6474827
W okrąg o równaniu 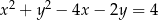 wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze
wpisano trójkąt równoramienny, w którym ramię tworzy z podstawą kąt o mierze 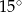 . Podstawa tego trójkąta ma długość
. Podstawa tego trójkąta ma długość
A) 1,5 B) 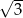 C) 3 D)
C) 3 D) 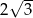
Rozwiązanie
Dane równanie okręgu możemy zapisać w postaci
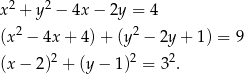
Jest to więc okrąg o środku 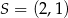 i promieniu
i promieniu 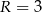 . Szkicujemy opisaną sytuację.
. Szkicujemy opisaną sytuację.
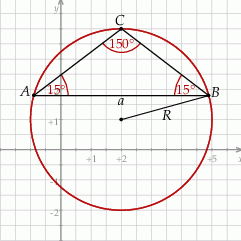
Pozostało teraz zastosować twierdzenie sinusów.
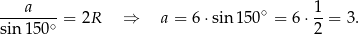
Odpowiedź: C

