Zadanie nr 6630763
W układzie współrzędnych dany jest trójkąt o wierzchołkach 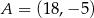 ,
, 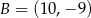 i
i 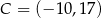 . Na boku
. Na boku 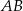 tego trójkąta wybrano punkt
tego trójkąta wybrano punkt 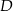 tak, że pole trójkąta
tak, że pole trójkąta 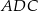 jest cztery razy mniejsze od pola trójkąta
jest cztery razy mniejsze od pola trójkąta 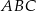 . Wówczas
. Wówczas
A) 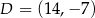 B)
B) 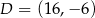 C)
C) 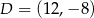 D)
D) 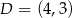
Rozwiązanie
Szkicujemy opisaną sytuację.
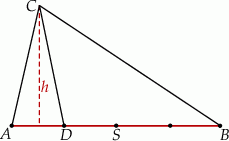
Zauważmy, że trójkąty 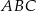 i
i 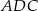 mają wspólną wysokość opuszczona z wierzchołka
mają wspólną wysokość opuszczona z wierzchołka 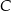 , więc podana informacja o stosunku ich pól oznacza, że
, więc podana informacja o stosunku ich pól oznacza, że 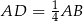 . Punkt
. Punkt 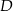 jest więc środkiem odcinka
jest więc środkiem odcinka 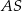 , gdzie
, gdzie
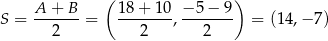
jest środkiem odcinka 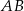 . Mamy zatem
. Mamy zatem
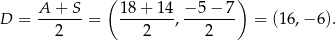
Odpowiedź: B

