Zadanie nr 7184294
Punkt 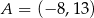 jest wierzchołkiem kwadratu
jest wierzchołkiem kwadratu 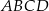 , którego przekątne przecinają się w punkcie
, którego przekątne przecinają się w punkcie 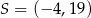 . Punkty
. Punkty 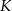 i
i 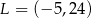 są odpowiednio środkami odcinków
są odpowiednio środkami odcinków 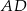 i
i 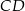 . Punkt
. Punkt 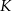 ma współrzędne
ma współrzędne
A) 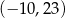 B)
B) 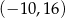 C)
C) 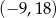 D)
D) 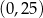
Rozwiązanie
Sposób I
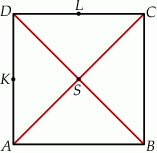
Przekątne kwadratu dzielą się na połowy, więc ich punkt przecięcia 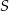 jest środkiem odcinka
jest środkiem odcinka 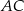 .
.
Mamy zatem
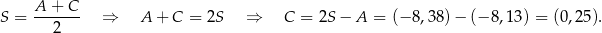
Punkt 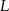 jest środkiem odcinka
jest środkiem odcinka 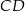 , więc
, więc
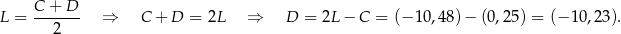
Stąd
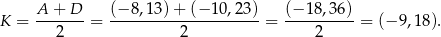
Sposób II
Zauważmy, że 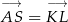 , więc
, więc
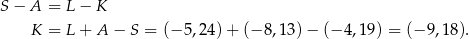
Odpowiedź: C

