Zadanie nr 7297962
W kole poprowadzono cięciwę tworzącą ze średnicą kąt 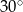 . Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
. Cięciwa dzieli średnicę na dwa odcinki o długościach 6 cm i 2 cm. Zatem odległość środka okręgu od cięciwy jest równa
A) 2 cm B) 1 cm C) 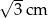 D)
D) 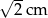
Rozwiązanie
Zaczynamy od rysunku
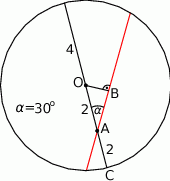
Ponieważ cięciwa dzieli średnicę na dwie części o długościach 6 cm i 2 cm, więc cała średnica ma długość 8 cm. Zatem promień okręgu ma długość 4 cm. Stąd
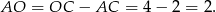
Wiemy ponadto, że
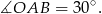
Chcemy obliczyć odległość punktu  od cięciwy. Odległość ta jest równa długości odcinka
od cięciwy. Odległość ta jest równa długości odcinka  prostopadłego do cięciwy i przechodzącego przez punkt
prostopadłego do cięciwy i przechodzącego przez punkt  . Liczymy
. Liczymy
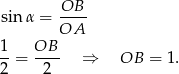
Odpowiedź: B

