Zadanie nr 7509793
Z odcinków o długościach: 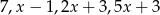 można zbudować trapez równoramienny. Wynika stąd, że
można zbudować trapez równoramienny. Wynika stąd, że
A) 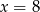 B)
B) 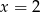 C)
C)  D)
D) 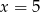
Rozwiązanie
Nie wiemy, które dwa boki czworokąta mają być równe, więc sprawdzamy kolejne możliwości.
Równości 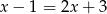 ,
, 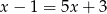 i
i 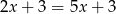 prowadzą do tego, że
prowadzą do tego, że 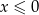 , co jest oczywiście niemożliwe. W takim razie jednym z ramion trapezu musi być odcinek długości 7.
, co jest oczywiście niemożliwe. W takim razie jednym z ramion trapezu musi być odcinek długości 7.
Jeżeli 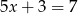 , to
, to 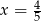 i wtedy
i wtedy 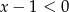 .
.
Jeżeli 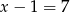 , to
, to 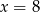 . To oznacza, że otrzymujemy czworokąt o bokach: 7, 7, 19, 43, co nie jest możliwe, bo
. To oznacza, że otrzymujemy czworokąt o bokach: 7, 7, 19, 43, co nie jest możliwe, bo 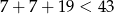 .
.
W takim razie 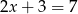 i
i 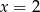 . Otrzymujemy w tej sytuacji czworokąt o bokach: 7, 1, 7, 13.
. Otrzymujemy w tej sytuacji czworokąt o bokach: 7, 1, 7, 13.
Odpowiedź: B

