Zadanie nr 7639090
Dany jest czworokąt 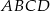 wpisany w okrąg o środku
wpisany w okrąg o środku 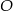 . Wówczas, jeśli
. Wówczas, jeśli 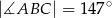 , to miara kąta
, to miara kąta 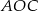 jest równa
jest równa
A) 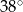 B)
B) 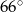 C)
C) 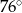 D)
D) 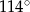
Rozwiązanie
Zaczynamy od rysunku
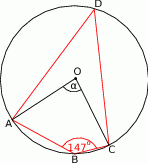
Sposób I
Patrzymy na kąty oparte na łuku 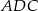 .
.
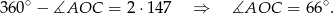
Sposób I
Liczymy
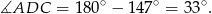
Zatem
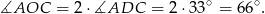
Odpowiedź: B

