Zadanie nr 7921222
Sinus kąta ostrego równoległoboku jest równy  . Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
. Suma cosinusów wszystkich kątów wewnętrznych tego równoległoboku jest równa
A) 0 B) 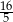 C)
C) 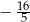 D)
D) 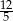
Rozwiązanie
Szkicujemy równoległobok.
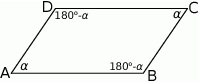
Sposób I
Z jedynki trygonometrycznej obliczamy 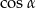
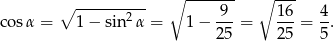
Obliczamy jeszcze cosinus kąta rozwartego równoległoboku
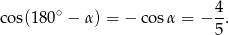
W takim interesująca nas suma cosinusów jest równa
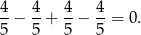
Sposób II
Zauważmy, że
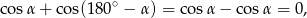
więc suma cosinusów kątów wewnętrznych w równoległoboku jest zawsze równa 0.
Odpowiedź: A

