Zadanie nr 8154645
Podstawą graniastosłupa prostego czworokątnego 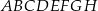 jest kwadrat
jest kwadrat 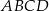 o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa
o polu 4 (zobacz rysunek). Objętość graniastosłupa jest równa 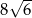 . Miara kąta
. Miara kąta 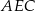 jest równa
jest równa
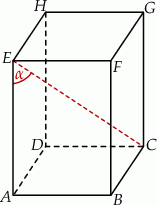
A) 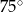 B)
B) 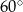 C)
C) 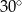 D)
D) 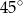
Rozwiązanie
Jeżeli pole kwadratu w podstawie jest równe 4, to jego bok ma długość 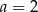 , a przekątna długość
, a przekątna długość 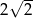 .
.
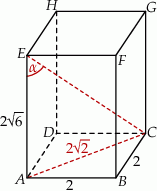
Z podanej objętości obliczamy długość krawędzi bocznej 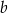 .
.
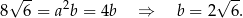
Patrzymy teraz na trójkąt prostokątny 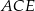 .
.
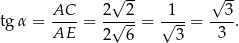
Zatem 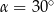 .
.
Odpowiedź: C

