Zadanie nr 8282910
Wskaż równanie okręgu stycznego do prostej 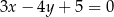 .
.
A) 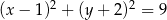 B)
B) 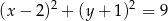
C) 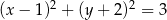 D)
D) 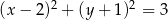
Rozwiązanie
Wśród podanych odpowiedzi są okręgi o środkach 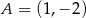 i
i 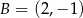 .
.
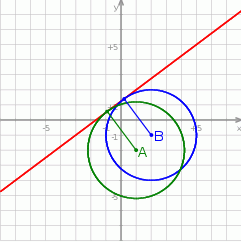
Korzystając ze wzoru na odległość punktu 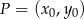 od prostej
od prostej 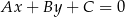 :
:
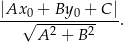
obliczamy odległości punktów 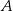 i
i 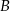 od danej prostej. Mamy odpowiednio
od danej prostej. Mamy odpowiednio
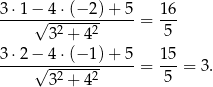
To oznacza, że okręgi o środkach 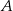 i
i 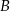 , które są styczne do danej prostej mają odpowiednio równania
, które są styczne do danej prostej mają odpowiednio równania
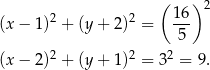
Odpowiedź: B

