Zadanie nr 8333757
Pole trójkąta o bokach długości 8 oraz 15 i kącie między nimi o mierze 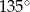 jest równe
jest równe
A) 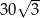 B)
B) 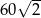 C)
C) 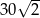 D)
D) 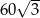
Rozwiązanie
Rozpoczynamy od rysunku.
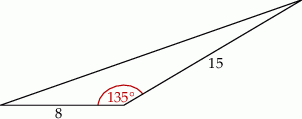
Na mocy wzoru 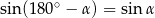 mamy
mamy
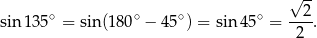
Ze wzoru na pole z sinusem mamy
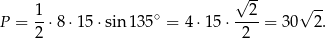
Odpowiedź: C
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Pole trójkąta o bokach długości 8 oraz 15 i kącie między nimi o mierze 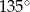 jest równe
jest równe
A) 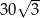 B)
B) 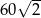 C)
C) 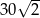 D)
D) 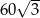
Rozpoczynamy od rysunku.

Na mocy wzoru 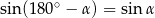 mamy
mamy
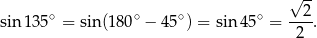
Ze wzoru na pole z sinusem mamy
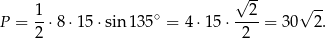
Odpowiedź: C
