Zadanie nr 8446828
Wysokość trójkąta równobocznego 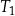 jest równa
jest równa 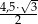 . Wysokość trójkąta równobocznego
. Wysokość trójkąta równobocznego 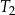 jest równa
jest równa 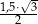 . Stosunek pola trójkąta
. Stosunek pola trójkąta 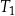 do pola trójkąta
do pola trójkąta 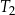 jest równy
jest równy
| A) 3, | B) 9, |
ponieważ
| 1) | bok trójkąta 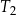 jest 9 razy krótszy od boku trójkąta jest 9 razy krótszy od boku trójkąta 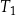 . . |
| 2) | wysokość trójkąta 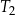 jest 3 razy krótsza od wysokości trójkąta jest 3 razy krótsza od wysokości trójkąta 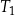 . . |
| 3) | bok trójkąta 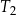 jest o 3 krótszy od boku trójkąta jest o 3 krótszy od boku trójkąta 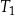 . . |
Rozwiązanie
Sposób I
Pole trójkąta zmienia się jak kwadrat skali podobieństwa, która w naszym przypadku jest równa
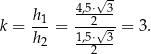
Stosunek pól jest więc równy 9.
Sposób II
Wysokość trójkąta równobocznego o boku  jest równa
jest równa
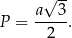
W takim razie trójkąt  ma bok długości
ma bok długości 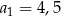 , a trójkąt
, a trójkąt 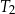 bok długości
bok długości 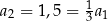 . To oznacza, że trójkąt
. To oznacza, że trójkąt 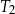 jest 3 razy mniejszy od trójkąta
jest 3 razy mniejszy od trójkąta 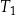 . Jego pole jest więc 9 razy mniejsze.
. Jego pole jest więc 9 razy mniejsze.
Odpowiedź: B, 2

