Zadanie nr 8646781
Dany jest trójkąt 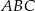 , w którym
, w którym 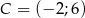 ,
, ![−→ CB = [4;− 2]](https://img.zadania.info/zad/8646781/HzadT2x.gif) oraz środek ciężkości
oraz środek ciężkości 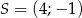 . Współrzędne wierzchołka
. Współrzędne wierzchołka 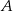 są równe
są równe
A) 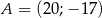 B)
B) 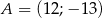 C)
C) 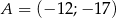 D)
D) 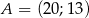
Rozwiązanie
Szkicujemy opisaną sytuację.
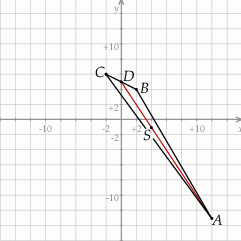
Obliczamy najpierw współrzędne środka 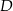 boku
boku 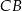 .
.
![−→ D = C + 1-CB = (− 2,6)+ [2,− 1] = (0,5). 2](https://img.zadania.info/zad/8646781/HzadR3x.gif)
Korzystamy teraz z faktu, że środek ciężkości 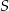 dzieli środkową
dzieli środkową 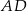 w stosunku 2 : 1.
w stosunku 2 : 1.
![−→ −→ AD = 3SD = 3(D − S) = 3[− 4,6] = [− 12,18].](https://img.zadania.info/zad/8646781/HzadR6x.gif)
To pozwala łatwo obliczyć współrzędne punktu 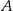 .
.
![−→ −→ AD = D − A ⇒ A = D − AD = (0,5) − [− 12,18] = (12,− 13 ).](https://img.zadania.info/zad/8646781/HzadR8x.gif)
Odpowiedź: B

