Zadanie nr 8812442
W ostrosłupie prawidłowym czworokątnym krawędź boczna jest 3 razy dłuższa od krawędzi podstawy. Wynika stąd, że cosinus kąta nachylenia ściany bocznej do płaszczyzny podstawy tego ostrosłupa jest równy
A) 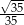 B)
B) 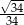 C)
C) 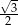 D)
D) 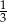
Rozwiązanie
Niech 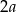 oznacza długość krawędzi podstawy ostrosłupa.
oznacza długość krawędzi podstawy ostrosłupa.
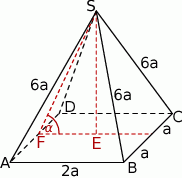
W trójkącie 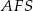 mamy
mamy
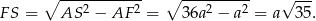
W podstawie ostrosłupa jest kwadrat, więc 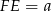 i interesujący nas cosinus jest równy
i interesujący nas cosinus jest równy
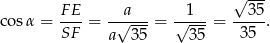
Odpowiedź: A

