Zadanie nr 8819793
Okrąg o środku w punkcie 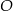 jest wpisany w trójkąt
jest wpisany w trójkąt 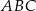 . Wiadomo, że
. Wiadomo, że 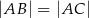 i
i 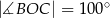 (zobacz rysunek).
(zobacz rysunek).
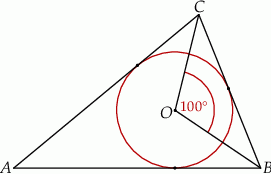
Miara kąta 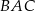 jest równa
jest równa
A) 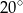 B)
B) 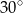 C)
C) 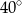 D)
D) 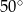
Rozwiązanie
Oznaczmy 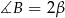 ,
, 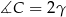 .
.
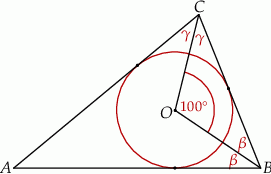
Środek okręgu wpisanego w trójkąt, to punkt przecięcia się dwusiecznych kątów tego trójkąta, więc odcinki 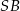 i
i 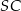 dzielą kąty przy wierzchołkach
dzielą kąty przy wierzchołkach 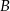 i
i 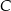 na połowy. Zatem
na połowy. Zatem
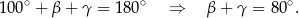
Teraz patrzymy na trójkąt 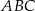 .
.
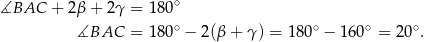
Odpowiedź: A

