Zadanie nr 9055353
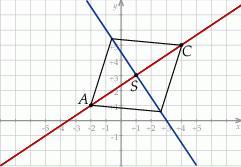
Na rysunku jest przedstawiona prosta zawierająca przekątną 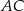 rombu
rombu 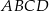 oraz wierzchołki
oraz wierzchołki 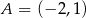 i
i 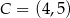 tego rombu.
tego rombu.
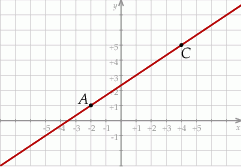
Wskaż równanie prostej zawierającej przekątną 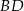 tego rombu.
tego rombu.
A) 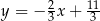 B)
B) 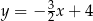 C)
C) 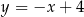 D)
D) 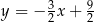
Rozwiązanie
Sposób I
Ponieważ przekątne rombu są prostopadłe i dzielą się na połowy, to prosta 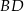 jest prostopadła do podanej przekątnej
jest prostopadła do podanej przekątnej 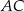 i przechodzi przez środek rombu
i przechodzi przez środek rombu 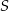 .
.
Punkt 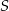 jest środkiem odcinka
jest środkiem odcinka 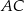 , więc
, więc
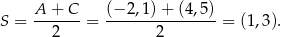
Wyznaczmy teraz równanie prostej 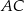 – szukamy prostej w postaci
– szukamy prostej w postaci 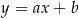 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 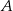 i
i 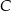 .
.
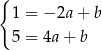
Odejmujemy od drugiego równania pierwsze i mamy 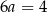 , czyli
, czyli 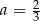 . Współczynnika
. Współczynnika 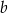 nie wyznaczamy, bo nie jest nam potrzebny.
nie wyznaczamy, bo nie jest nam potrzebny.
Prosta 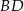 ma więc równanie postaci
ma więc równanie postaci 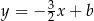 . Współczynnik
. Współczynnik 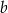 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 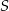 .
.
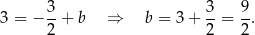
Sposób II
Szukana przekątna 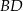 to dokładnie symetralna odcinka
to dokładnie symetralna odcinka 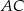 . Jej równanie możemy wyznaczyć szukając punktów
. Jej równanie możemy wyznaczyć szukając punktów 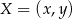 , których odległości od
, których odległości od 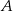 i
i 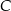 są takie same.
są takie same.
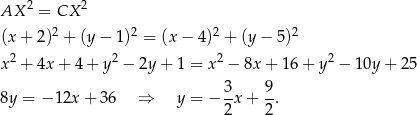
Odpowiedź: D

