Zadanie nr 9254646
Dany jest trójkąt równoramienny 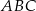 o kącie między ramionami
o kącie między ramionami 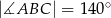 . Punkt
. Punkt 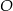 jest środkiem okręgu wpisanego w ten trójkąt. Prosta
jest środkiem okręgu wpisanego w ten trójkąt. Prosta 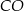 przecina podstawę
przecina podstawę 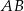 w punkcie
w punkcie 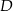 . Miara kąta
. Miara kąta 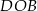 jest równa
jest równa
A) 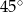 B)
B) 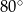 C)
C) 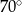 D)
D) 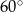
Rozwiązanie
Zaczynamy od rysunku
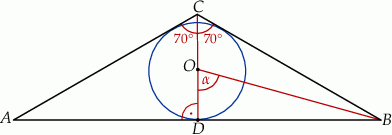
Ponieważ miara kąta 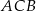 wynosi
wynosi 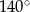 i trójkąt
i trójkąt 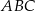 jest równoramienny, więc
jest równoramienny, więc
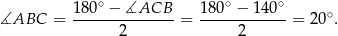
Prosta 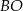 jest dwusieczną kąta
jest dwusieczną kąta 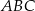 , więc
, więc
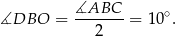
Stąd
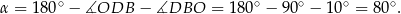
Odpowiedź: B

