Zadanie nr 9296307
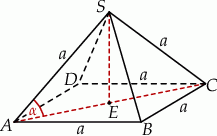
Podstawą ostrosłupa prawidłowego czworokątnego 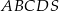 jest kwadrat
jest kwadrat 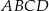 . Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
. Wszystkie ściany boczne tego ostrosłupa są trójkątami równobocznymi.
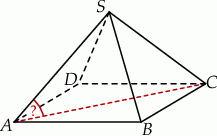
Miara kąta 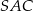 jest równa
jest równa
A) 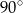 B)
B) 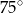 C)
C) 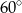 D)
D) 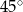
Rozwiązanie
Niech  oznacza długość każdej z krawędzi ostrosłupa.
oznacza długość każdej z krawędzi ostrosłupa.
Sposób I
W podstawie ostrosłupa jest kwadrat, więc
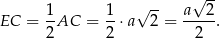
Z trójkąta 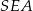 mamy więc
mamy więc
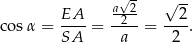
To oznacza, że 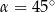 .
.
Sposób II
Zauważmy, że trójkąty 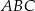 i
i 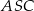 mają równe długości boków, więc są przystające. W takim razie
mają równe długości boków, więc są przystające. W takim razie
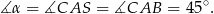
Odpowiedź: D

