Zadanie nr 9340676
Podstawą graniastosłupa prawidłowego czworokątnego jest kwadrat o boku długości 3, a przekątna ściany bocznej ma długość 4 (zobacz rysunek). Kąt, jaki tworzą przekątne ścian bocznych tego graniastosłupa wychodzące z jednego wierzchołka, ma miarę  .
.
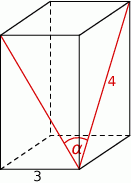
Wtedy wartość 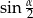 jest równa
jest równa
A)  B)
B) 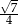 C)
C) 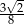 D)
D) 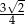
Rozwiązanie
Niech 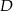 będzie środkiem górnej podstawy.
będzie środkiem górnej podstawy.
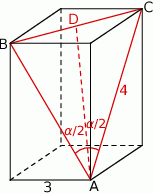
Trójkąt 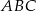 jest równoramienny, więc odcinek
jest równoramienny, więc odcinek 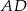 jest dwusieczną kąta
jest dwusieczną kąta 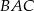 . Mamy zatem
. Mamy zatem
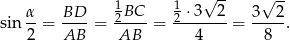
Odpowiedź: C

