Zadanie nr 9368231
Punkty 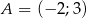 ,
, 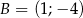 ,
, 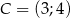 są kolejnymi wierzchołkami równoległoboku
są kolejnymi wierzchołkami równoległoboku 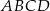 . Równanie prostej zawierającej bok
. Równanie prostej zawierającej bok 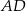 tego równoległoboku ma postać
tego równoległoboku ma postać
A) 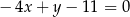 B)
B) 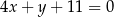
C) 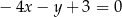 D)
D) 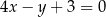
Rozwiązanie
Szkicujemy opisaną sytuację.
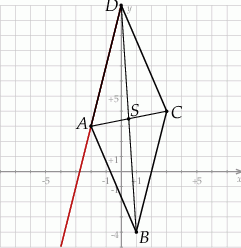
Sposób I
Prosta 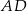 jest równoległa
jest równoległa 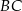 i przechodzi przez
i przechodzi przez 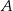 . Zacznijmy od wyznaczenia współczynnika kierunkowego prostej
. Zacznijmy od wyznaczenia współczynnika kierunkowego prostej 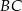 . Szukamy prostej w postaci
. Szukamy prostej w postaci 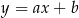 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 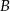 i
i 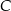 .
.
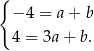
Odejmujemy od drugiego równania pierwsze i mamy
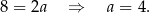
W takim razie prosta 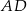 ma równanie postaci
ma równanie postaci 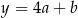 . Współczynnik
. Współczynnik 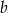 wyznaczamy podstawiając współrzędne punktu
wyznaczamy podstawiając współrzędne punktu 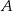 .
.

Prosta 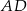 ma więc równanie
ma więc równanie 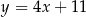 .
.
Sposób II
Środek 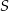 równoległoboku ma współrzędne
równoległoboku ma współrzędne
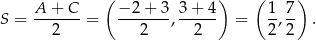
To pozwala wyznaczyć współrzędne punktu 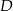
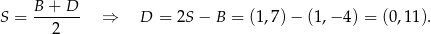
Piszemy teraz równanie prostej 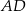 – szukamy prostej w postaci
– szukamy prostej w postaci 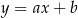 i podstawiamy współrzędne punktów
i podstawiamy współrzędne punktów 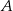 i
i 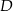 .
.
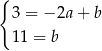
Stąd
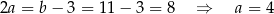
i prosta 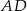 ma równanie
ma równanie
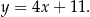
Odpowiedź: A

