Zadanie nr 9391514
Równanie okręgu wpisanego w romb o wierzchołkach 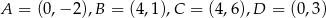 ma postać
ma postać
A) 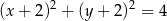 B)
B) 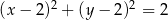
C) 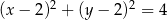 D)
D) 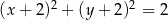
Rozwiązanie
Jeżeli naszkicujemy romb, to jest jasne, że środkiem okręgu wpisanego jest środek przekątnej 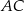 (czyli punkt przecięcia przekątnych).
(czyli punkt przecięcia przekątnych).
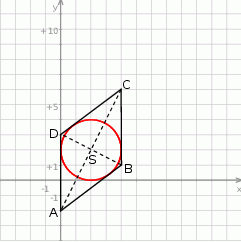
Zatem
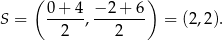
Promień okręgu wpisanego jest równy odległości punktu 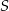 od osi
od osi 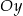 (bo zawiera ona bok
(bo zawiera ona bok 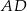 ) rombu, czyli jest równy 2. Zatem szukane równanie ma postać
) rombu, czyli jest równy 2. Zatem szukane równanie ma postać
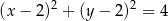
Odpowiedź: C

