Zadanie nr 9434312
Obwód trójkąta 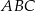 jest równy 40 cm. Punkt
jest równy 40 cm. Punkt 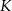 leży na boku
leży na boku 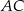 , a punkt
, a punkt 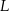 na boku
na boku 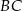 tak, że odcinek
tak, że odcinek 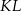 jest równoległy do boku
jest równoległy do boku 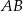 trójkąta i
trójkąta i 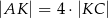 . Obwód trójkąta
. Obwód trójkąta 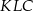 jest równy:
jest równy:
A) 10 cm B) 4 cm C) 8 cm D) 5 cm
Rozwiązanie
Naszkicujmy opisaną sytuację.
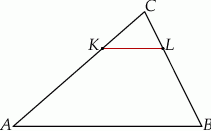
Proste 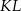 i
i 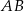 są równoległe, więc trójkąty
są równoległe, więc trójkąty 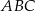 i
i 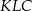 są podobne (bo mają równe kąty). Ponadto, z podanego stosunku odcinków
są podobne (bo mają równe kąty). Ponadto, z podanego stosunku odcinków 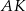 i
i 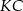 możemy odczytać, że skala podobieństwa jest równa
możemy odczytać, że skala podobieństwa jest równa
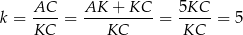
. Przypomnijmy, że stosunek obwodów figur podobnych w skali 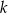 jest równy
jest równy 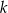 . Zatem
. Zatem
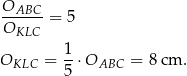
Odpowiedź: C

