Zadanie nr 9452504
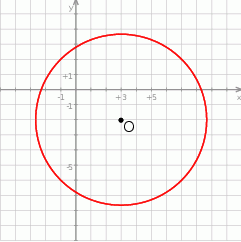
Punkt  jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
jest środkiem okręgu przedstawionego na rysunku. Równanie tego okręgu ma postać:
A) 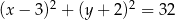 B)
B) 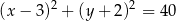
C) 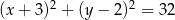 D)
D) 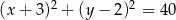
Rozwiązanie
Sposób I
Przedstawiony na obrazku okrąg to okrąg o środku 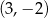 , więc ma postać
, więc ma postać
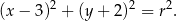
Zauważmy ponadto, że promień tego okręgu spełnia warunek: 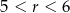 . Ponieważ
. Ponieważ 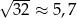 i
i 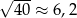 prawidłową odpowiedzią musi być
prawidłową odpowiedzią musi być
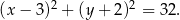
Sposób II
Jak w poprzednim sposobie zauważamy, że narysowany okrąg musi mieć równanie postaci
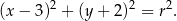
Zauważmy, ponadto, że okrąg ten przechodzi np. przez punkt 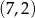 . To pozwala obliczyć
. To pozwala obliczyć 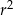 .
.
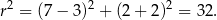
Odpowiedź: A

