Zadanie nr 9550875
Ile jest okręgów o promieniu 1, które są jednocześnie styczne do prostej 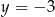 i wewnętrznie styczne do okręgu
i wewnętrznie styczne do okręgu 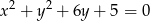 ?
?
A) 1 B) 2 C) 3 D) 4
Rozwiązanie
Zapiszmy równanie okręgu tak, aby było widać jaki ma środek i promień.
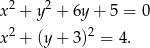
Jest to więc okrąg o środku w punkcie 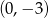 i promieniu 2.
i promieniu 2.
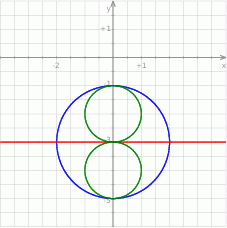
Jeżeli wykonamy szkicowy rysunek to widać, że są dwa okręgi spełniające warunki zadania: okręgi o środkach 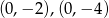 i promieniu 1.
i promieniu 1.
Odpowiedź: B

