Zadanie nr 9567444
Punkt 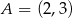 jest wierzchołkiem trójkąta równobocznego
jest wierzchołkiem trójkąta równobocznego 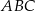 . Punkt
. Punkt 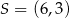 jest środkiem okręgu opisanego na trójkącie
jest środkiem okręgu opisanego na trójkącie 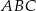 . Wskaż równanie okręgu wpisanego w trójkąt
. Wskaż równanie okręgu wpisanego w trójkąt 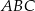 .
.
A) 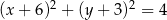 B)
B) 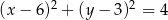
C) 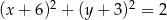 D)
D) 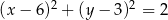
Rozwiązanie
Ponieważ
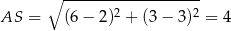
to promień okręgu opisanego na trójkącie 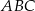 jest równy
jest równy 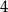 .
.
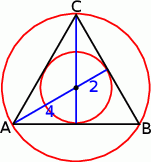
Promień okręgu wpisanego w trójkąt  jest dwa razy krótszy, czyli jest równy 2. Środkiem jest punkt
jest dwa razy krótszy, czyli jest równy 2. Środkiem jest punkt 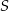 , zatem równanie ma postać
, zatem równanie ma postać
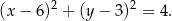
Odpowiedź: B

