Zadanie nr 9604716
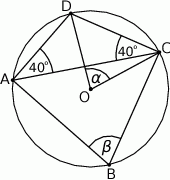
Punkty 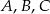 i
i 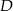 leżą na okręgu o środku
leżą na okręgu o środku 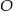 (zobacz rysunek). Miary zaznaczonych kątów
(zobacz rysunek). Miary zaznaczonych kątów  i
i 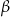 są odpowiednio równe
są odpowiednio równe
A) 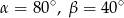 B)
B) 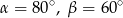 C)
C) 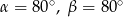 D)
D) 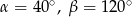
Rozwiązanie
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, to
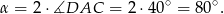
Miarę kąta 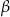 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Dorysujmy promień 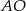 .
.
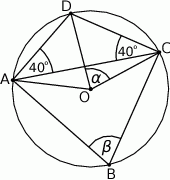
Ponownie korzystamy z tego, kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku.
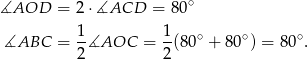
Sposób II
Korzystamy z tego, że w czworokącie wpisanym w okrąg sumy przeciwległych kątów są równe 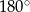 .
.
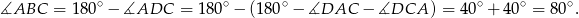
Odpowiedź: C

