Zadanie nr 9607404
Okrąg 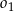 ma równanie
ma równanie 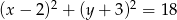 , a okrąg
, a okrąg 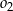 ma równanie
ma równanie 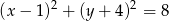 . Określ wzajemne położenie tych okręgów.
. Określ wzajemne położenie tych okręgów.
A) Te okręgi przecinają się w dwóch punktach.
B) Te okręgi są styczne.
C) Te okręgi nie mają punktów wspólnych oraz okrąg 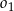 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 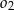 .
.
D) Te okręgi nie mają punktów wspólnych oraz okrąg 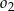 leży w całości wewnątrz okręgu
leży w całości wewnątrz okręgu 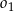 .
.
Rozwiązanie
Pierwszy okrąg ma środek 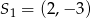 i promień
i promień 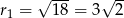 , a drugi ma środek
, a drugi ma środek 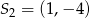 i promień
i promień 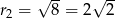 . Obliczmy jeszcze odległość między środkami okręgów.
. Obliczmy jeszcze odległość między środkami okręgów.
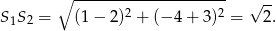
Ponieważ 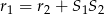 , okręgi są styczne wewnętrznie.
, okręgi są styczne wewnętrznie.
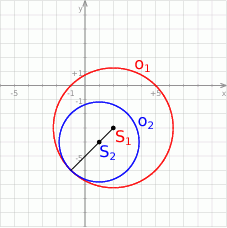
Odpowiedź: B

