Zadanie nr 9798162
W ostrosłupie prawidłowym czworokątnym, w którym wszystkie krawędzie mają tę samą długość, kąt między wysokością ostrosłupa, a jego krawędzią boczną ma miarę
A) 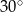 B)
B) 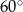 C)
C) 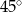 D)
D) 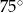
Rozwiązanie
Niech  oznacza długość każdej z krawędzi ostrosłupa.
oznacza długość każdej z krawędzi ostrosłupa.
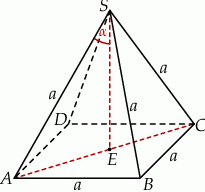
Sposób I
W podstawie ostrosłupa jest kwadrat, więc
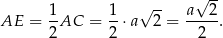
Z trójkąta 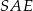 mamy więc
mamy więc
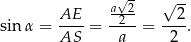
To oznacza, że 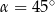 .
.
Sposób II
Zauważmy, że trójkąty 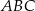 i
i 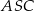 mają równe długości boków, więc są przystające. W takim razie
mają równe długości boków, więc są przystające. W takim razie
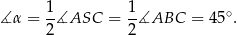
Odpowiedź: C

