Zadanie nr 2158799
Trapez 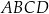 podzielono przekątną
podzielono przekątną 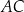 na dwa trójkąty. Punkty
na dwa trójkąty. Punkty 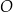 i
i 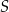 są środkami okręgów wpisanych w trójkąty
są środkami okręgów wpisanych w trójkąty 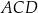 i
i 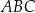 , a odcinek
, a odcinek 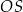 przecina przekątną
przecina przekątną 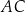 w punkcie
w punkcie 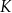 (zobacz rysunek). Stosunek długości okręgów o środkach
(zobacz rysunek). Stosunek długości okręgów o środkach 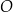 i
i 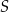 jest równy
jest równy  , a odcinek
, a odcinek 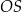 ma długość 24.
ma długość 24.
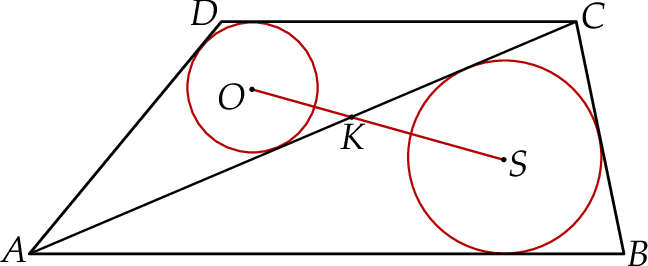
Wtedy
A) 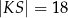 B)
B) 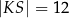 C)
C) 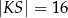 D)
D) 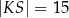
Rozwiązanie
Dorysujmy promienie 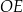 i
i 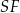 danych okręgów.
danych okręgów.
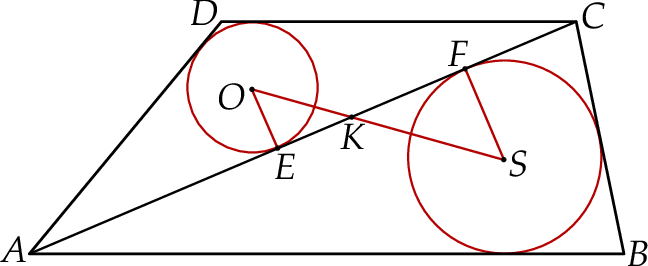
Zauważmy, że trójkąty prostokątne 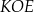 i
i 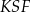 mają równe kąty. Są więc podobne i
mają równe kąty. Są więc podobne i
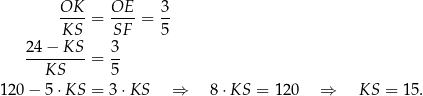
Odpowiedź: D

