Zadanie nr 2683786
Dany jest równoramienny trójkąt 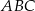 o kącie przy podstawie
o kącie przy podstawie 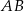 równym
równym 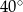 . Punkt
. Punkt 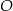 jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty
jest środkiem okręgu wpisanego w ten trójkąt. Przez punkty 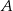 i
i 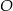 poprowadzono prostą, która przecięła bok
poprowadzono prostą, która przecięła bok 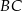 w punkcie
w punkcie 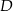 . Jeśli miara kąta
. Jeśli miara kąta 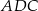 jest równa
jest równa  , to
, to
A) 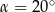 B)
B) 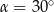 C)
C) 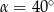 D)
D) 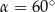
Rozwiązanie
Zaczynamy od rysunku
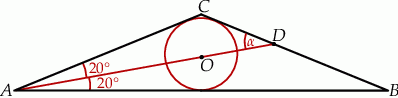
Trójkąt 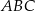 jest równoramienny, więc
jest równoramienny, więc
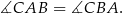
Stąd
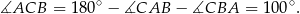
Odcinek 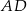 jes dwusieczną kąta
jes dwusieczną kąta 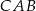 , więc
, więc
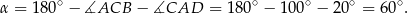
Odpowiedź: D

