Zadanie nr 3703347
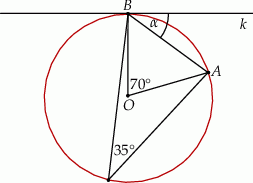
Na rysunku przedstawiono okrąg o środku 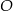 oraz kąt środkowy o mierze
oraz kąt środkowy o mierze 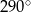 . Punkty
. Punkty 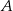 i
i 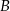 znajdują się na okręgu. Prosta
znajdują się na okręgu. Prosta 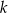 jest styczna do okręgu w punkcie
jest styczna do okręgu w punkcie 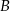 .
.
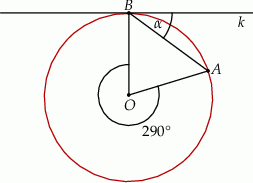
Miara kąta  jest równa
jest równa
A) 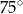 B)
B) 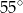 C)
C) 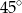 D)
D) 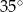
Rozwiązanie
Obliczamy najpierw miarę kąta wypukłego 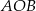
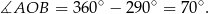
Sposób I
Zauważmy, że trójkąt 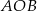 jest równoramienny, więc
jest równoramienny, więc
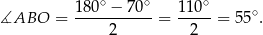
Styczna 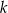 jest prostopadła do promienia
jest prostopadła do promienia 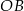 , więc
, więc
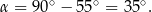
Sposób II
Tym razem skorzystamy z twierdzenia o stycznej.
Na mocy tego twierdzenia interesujący nas kąt  między sieczną i styczną ma taką samą miarę jak kąt wpisany oparty na cięciwie
między sieczną i styczną ma taką samą miarę jak kąt wpisany oparty na cięciwie 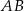 . Stąd
. Stąd

Odpowiedź: D

