Zadanie nr 5266844
Punkt 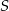 jest środkiem okręgu, na którym leżą punkty
jest środkiem okręgu, na którym leżą punkty 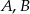 i
i 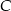 (patrz rysunek). Jeśli
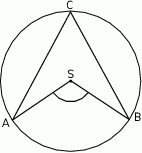
(patrz rysunek). Jeśli 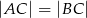 i miara kąta wypukłego
i miara kąta wypukłego 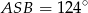 , to kąt wypukły
, to kąt wypukły 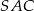 jest równy
jest równy
A) 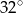 B)
B) 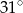 C)
C) 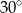 D)
D) 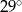
Rozwiązanie
Jeżeli dorysujemy promień 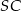 , to otrzymane trójkąty równoramienne
, to otrzymane trójkąty równoramienne 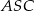 i
i 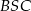 są przystające (bo mają równe długości boków).
są przystające (bo mają równe długości boków).
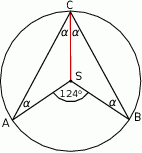
Możemy więc oznaczyć
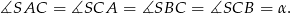
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, mamy
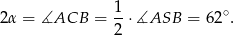
Stąd 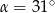 .
.
Odpowiedź: B

