Zadanie nr 5469163
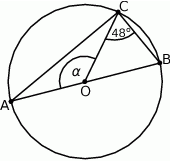
Na okręgu o środku w punkcie 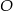 leży punkt
leży punkt 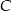 (zobacz rysunek). Odcinek
(zobacz rysunek). Odcinek 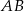 jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy
jest średnicą tego okręgu. Zaznaczony na rysunku kąt środkowy  ma miarę
ma miarę
A) 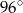 B)
B) 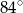 C)
C) 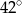 D)
D) 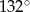
Rozwiązanie
Sposób I
Zauważmy, że trójkąt 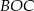 jest równoramienny, więc
jest równoramienny, więc
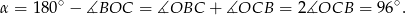
Sposób II
Korzystając z twierdzenia o kątach wpisanym i środkowym, mamy
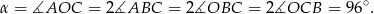
Sposób III
Kąt 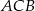 jest oparty na średnicy, więc
jest oparty na średnicy, więc
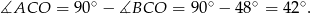
Teraz wystarczy zauważyć, że trójkąt  jest równoramienny. Mamy zatem
jest równoramienny. Mamy zatem
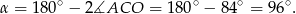
Odpowiedź: A

