Zadanie nr 5744045
Odcinek 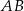 jest średnicą okręgu o środku
jest średnicą okręgu o środku 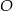 i promieniu
i promieniu  , a punkt
, a punkt 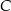 jest środkiem łuku o końcach
jest środkiem łuku o końcach 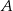 i
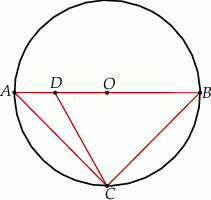
i 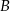 (zobacz rysunek). Na odcinku
(zobacz rysunek). Na odcinku 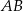 wybrano punkt
wybrano punkt 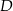 taki, że
taki, że 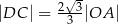 .
.
Pole trójkąta 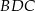 jest równe
jest równe
A) 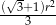 B)
B) 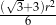 C)
C) 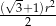 D)
D) 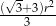
Rozwiązanie
Dorysujmy promień 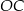 .
.
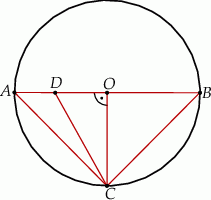
Trójkąt 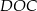 jest prostokątny oraz
jest prostokątny oraz 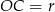 . Zatem
. Zatem
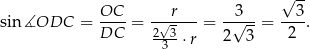
To oznacza, że 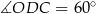 , czyli trójkąt
, czyli trójkąt 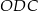 jest połówką trójkąta równobocznego. W szczególności
jest połówką trójkąta równobocznego. W szczególności
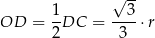
Korzystamy ze wzoru z sinusem na pole trójkąta
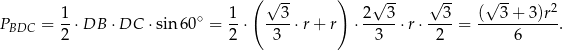
Odpowiedź: B

