Zadanie nr 6249569
Punkty 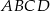 leżą na okręgu o środku
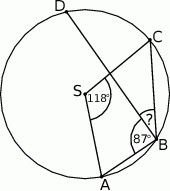
leżą na okręgu o środku 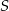 (zobacz rysunek). Miara kąta
(zobacz rysunek). Miara kąta 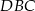 jest równa
jest równa
A) 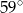 B)
B) 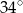 C)
C) 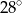 D)
D) 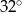
Rozwiązanie
Sposób I
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku, kąt 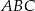 ma miarę dwa razy mniejszą od kąta wklęsłego
ma miarę dwa razy mniejszą od kąta wklęsłego 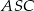 , więc
, więc
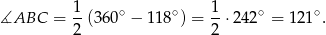
Stąd
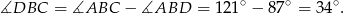
Sposób II
Niech 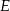 będzie punktem okręgu jak na rysunku poniżej.
będzie punktem okręgu jak na rysunku poniżej.
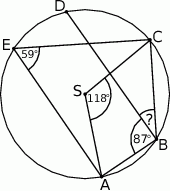
Ponieważ kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku,
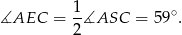
Czworokąt 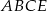 jest wpisany w okrąg, więc
jest wpisany w okrąg, więc
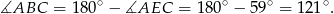
Stąd
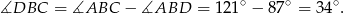
Odpowiedź: B

