Zadanie nr 6490250
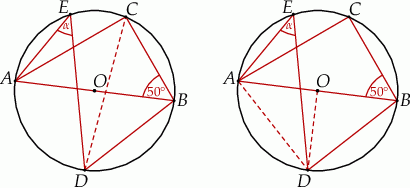
Punkty 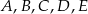 leżą na okręgu o środku
leżą na okręgu o środku 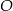 , przy czym
, przy czym 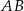 jest średnicą tego okręgu,
jest średnicą tego okręgu, 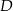 jest środkiem łuku
jest środkiem łuku 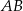 oraz
oraz 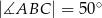 .
.
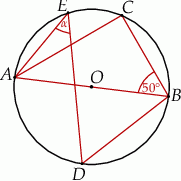
Miara kąta oznaczonego na rysunku literą  jest równa
jest równa
A) 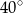 B)
B) 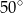 C)
C) 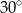 D)
D) 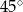
Rozwiązanie
Sposób I
Zauważmy najpierw, że 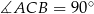 jako kąt wpisany oparty na średnicy
jako kąt wpisany oparty na średnicy  .
.
Ponieważ kąty wpisane oparte na tym samym łuku mają równe miary, to
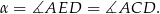
Wiemy też, że łuki 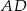 i
i 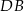 mają tą samą długość, więc
mają tą samą długość, więc
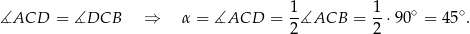
Sposób II
Ponieważ 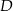 jest środkiem łuku
jest środkiem łuku 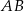 , trójkąt
, trójkąt 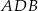 jest równoramienny i prostokątny (bo kąt
jest równoramienny i prostokątny (bo kąt 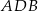 jest oparty na średnicy). Zatem
jest oparty na średnicy). Zatem
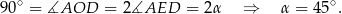
Skorzystaliśmy z tego, że kąt środkowy jest dwa razy większy od kąta wpisanego opartego na tym samym łuku.
Odpowiedź: D

