/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 6675426

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątna 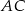AC prostokąta 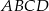ABCD ma długość 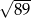√ --- 89 , a bok 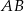AB jest o 3 dłuższy od boku 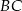BC . Oblicz pole prostokąta.
A) 8 B) 40 C) 5 D) 20

Rozwiązanie

Jeżeli oznaczymy 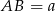AB = a to BC = a− 3 .

PIC

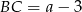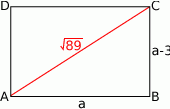
Stosując twierdzenie Pitagorasa w trójkącie 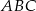ABC mamy

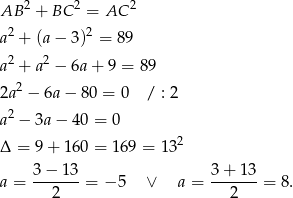
2 2 2 AB + BC = AC a2 + (a− 3)2 = 89 a2 + a2 − 6a+ 9 = 89 2 2a − 6a − 80 = 0 / : 2 a2 − 3a− 40 = 0 2 Δ = 9+ 160 = 169 = 13 3 − 13 3+ 13 a = -------= − 5 ∨ a = -------= 8. 2 2

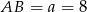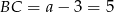Zatem AB = a = 8 i BC = a − 3 = 5 i pole jest równe

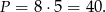
P = 8 ⋅5 = 4 0.

 
Odpowiedź: B

Wersja PDF