Zadanie nr 7354734
Na okręgu o środku w punkcie 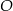 wybrano trzy punkty
wybrano trzy punkty 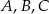 tak, że
tak, że 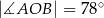 ,
, 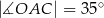 . Cięciwa
. Cięciwa 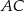 przecina promień
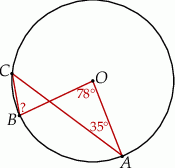
przecina promień 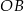 (zobacz rysunek). Wtedy miara
(zobacz rysunek). Wtedy miara 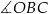 jest równa
jest równa
A) 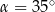 B)
B) 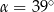 C)
C) 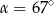 D)
D) 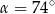
Rozwiązanie
Niech 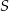 będzie punktem wspólnym odcinków
będzie punktem wspólnym odcinków 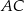 i
i 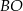 .
.
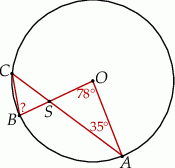
Korzystamy z twierdzenia o kątach wpisanym i środkowym
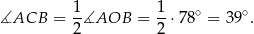
Ponadto
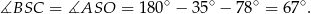
Zatem
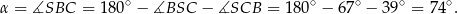
Odpowiedź: D

