/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 7514424

Dodaj do ulubionych
Dodaj do rozwiązanych

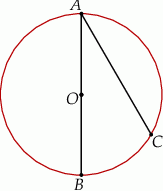
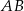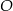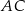Odcinek AB jest średnicą okręgu o środku w punkcie O i promieniu r (zobacz rysunek). Cięciwa AC ma długość 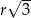√ -- r 3 , więc

PIC

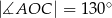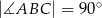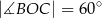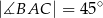
A) |∡AOC | = 130∘ B) |∡ABC | = 90∘ C) |∡BOC | = 60∘ D) |∡BAC | = 45∘

Rozwiązanie

Ponieważ 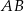AB jest średnicą okręgu, to trójkąt 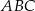ABC jest prostokątny.

PIC

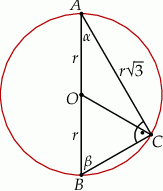
W szczególności

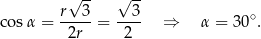
√ -- √ -- cos α = r--3-= --3- ⇒ α = 30∘. 2r 2

Trójkąt 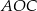AOC jest równoramienny, więc

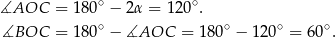
∘ ∘ ∡AOC = 180 − 2α = 120 . ∡BOC = 180∘ − ∡AOC = 18 0∘ − 120∘ = 60∘ .

 
Odpowiedź: C

Wersja PDF