Zadanie nr 8405682
Punkty 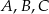 leżą na okręgu o środku
leżą na okręgu o środku  (zobacz rysunek). Ponadto
(zobacz rysunek). Ponadto 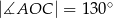 oraz
oraz 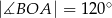 .
.
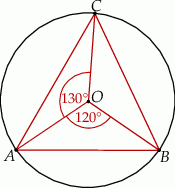
Miara kąta wewnętrznego 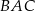 trójkąta
trójkąta 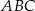 jest równa
jest równa
A) 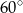 B)
B) 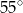 C)
C) 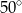 D)
D) 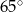
Rozwiązanie
Sposób I
Zauważmy, że każdy z trójkątów 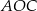 i
i  jest równoramienny. Mamy zatem
jest równoramienny. Mamy zatem
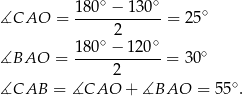
Sposób II
Korzystamy z twierdzenia o kątach wpisanym i środkowym i mamy
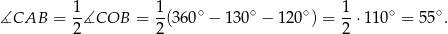
Odpowiedź: B

