/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 8459011

Dodaj do ulubionych
Dodaj do rozwiązanych

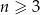W każdym n –kącie wypukłym (n ≥ 3 ) liczba przekątnych jest równa 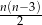n(n−-3) 2 . Wielokątem wypukłym, w którym liczba przekątnych jest o 25 większa od liczby boków, jest
A) siedmiokąt. B) dziesięciokąt. C) dwunastokąt. D) piętnastokąt.

Rozwiązanie

Oznaczmy przez n szukaną liczbę boków. Z podanego wzoru na liczbę przekątnych n –kąta wypukłego otrzymujemy równanie

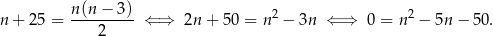
n + 25 = n(n-−-3)- ⇐ ⇒ 2n + 50 = n2 − 3n ⇐ ⇒ 0 = n2 − 5n − 50. 2

Rozwiązujemy otrzymane równanie kwadratowe.

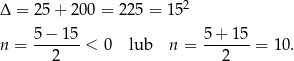
Δ = 2 5+ 200 = 225 = 152 n = 5-−-15-< 0 lub n = 5+--15-= 1 0. 2 2

 
Odpowiedź: B

Wersja PDF