Zadanie nr 8737497
Punkt 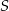 jest środkiem okręgu.
jest środkiem okręgu.
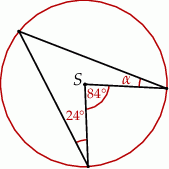
Miara kąta  wynosi
wynosi
A) 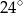 B)
B) 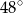 C)
C) 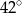 D)
D) 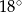
Rozwiązanie
Dorysujmy promień 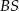 okręgu.
okręgu.
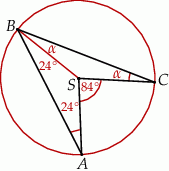
Sposób I
Zauważmy, że trójkąty 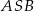 i
i 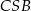 są równoramienne, więc
są równoramienne, więc
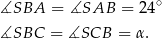
Mamy stąd
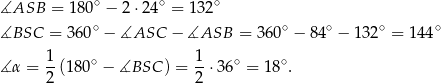
Sposób II
Korzystamy z zależności między kątami środkowym i wpisanym opartymi na tym samym łuku.
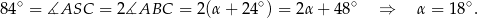
Sposób III
Zauważmy najpierw, że kąty 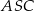 i
i 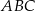 są oparte na tym samym łuku, więc
są oparte na tym samym łuku, więc
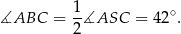
Teraz skorzystamy z tego, że suma kątów w czworokącie (nawet w takim, który nie jest wypukły) jest równa 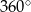 . Patrzymy na czworokąt
. Patrzymy na czworokąt 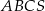 .
.
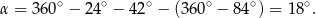
Odpowiedź: D

