/Szkoła średnia/Zadania testowe/Geometria/Planimetria

Zadanie nr 9321689

Dodaj do ulubionych
Dodaj do rozwiązanych

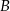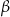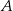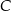W okręgu o środku w punkcie B kąt środkowy α i kąt wpisany β oparte są na tym samym łuku wyznaczonym przez punkty A i C leżące na okręgu. Suma miar tych kątów jest równa kątowi prostemu. Wierzchołek kąta 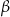β znajduje się w punkcie 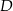D . Wynika stąd, że trójkąt
A) 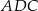ADC jest równoboczny B) 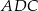ADC jest prostokątny
C) 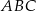ABC jest równoboczny D) 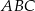ABC jest prostokątny

Rozwiązanie

Zaczynamy od rysunku

PIC

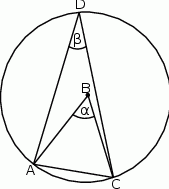
Wyznaczamy miary kątów α i β

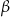
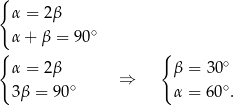
{ α = 2β α+ β = 90∘ { { α = 2β β = 3 0∘ ∘ ⇒ ∘ 3β = 90 α = 60 .

Ponieważ trójkąt 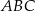ABC jest równoramienny i 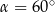α = 60 ∘ , więc 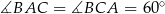∡BAC = ∡BCA = 60∘ . Zatem trójkąt 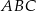ABC jest równoboczny.  
Odpowiedź: C

Wersja PDF